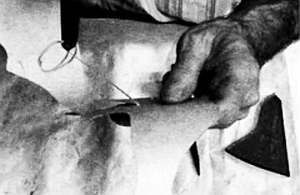
Ножницы с тройным лезвием обеспечивают нужный зазор постоянной ширины в 1,2 мм.

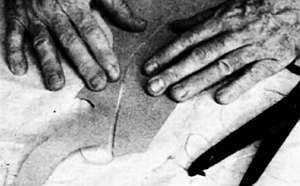
Два элемента рисунка соединяются с нужным зазором в 1,2 мм.

Перенос кривых также осуществляется автоматически с помощью гибкого лекала — резиновой полоски с металлическим сердечником, сохраняющей придаваемую ей форму. Гибкое лекало позволяет легко преобразовать дуги окружностей объемных фигур в отрезки той же длины на плоскости.

Гибкое лекало сохраняет придаваемую ему форму.

Еще одна геометрическая задача, с которой сталкиваются витражисты, заключается в воспроизведении пропорциональных кривых. Эта задача решается при помощи циркуля, как показано на следующей странице. Кривые пропорциональны, если заключенный между ними отрезок перпендикуляра, пересекающего обе кривые, имеет постоянную длину.

Циркуль указывает расстояние между двумя соответствующими точками пропорциональных кривых.

Циркуль указывает такое же расстояние между двумя другими точками пропорциональных кривых.

Обход кривых, расположенных на одинаковом расстоянии друг от друга, при помощи циркуля.

Пропорциональны ли две параллельные кривые? Параллельны ли две пропорциональные кривые?

В случае с ломаными линиями понятия параллельности и пропорциональности эквивалентны, так как любая ломаная есть часть многоугольника, а стороны подобных многоугольников параллельны. Это же верно и для дуг окружности. В таких случаях мысленное представление параллельных и пропорциональных кривых одинаково. Впрочем, если мы рассмотрим предельный случай, то заметим, что интуитивные представления о параллелизме и пропорциональности отличаются. К примеру, две следующие кривые параллельны в том смысле, что перпендикуляр, проведенный к первой из них в любой ее точке, будет перпендикуляром и ко второй, а часть этого перпендикуляра, заключенная между кривыми, всегда будет иметь одинаковую длину — иными словами, эти кривые располагаются на одинаковом расстоянии друг от друга. Но ни одна из них не является уменьшенной или увеличенной копией другой, как в случае с пропорциональными кривыми.

Кривая, параллельная данной, не сохраняет углы исходной кривой.

На следующем рисунке можно четко увидеть, чем отличается исходная кривая или ломаная от линии, параллельной ей и расположенной на определенном расстоянии. Существуют две траектории, или кривые, параллельные углу прямоугольника, — внешняя и внутренняя. На внешней траектории угол исчезает, на внутренней образуется петля.

Внутренняя и внешняя параллели углу прямоугольника.

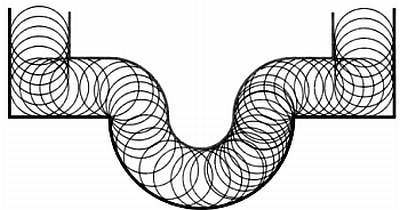
Продолжение описанной выше задачи можно увидеть в решетке церкви Сан-Феликс в городе Сабадель: в каждую из четырех внутренних окружностей вписано еще по четыре окружности.

Фрагмент розы в церкви Сан-Феликс в городе Сабадель в провинции Барселона.

Вы видите окружность, в которую вписаны четыре окружности меньшего размера, касающиеся друг друга. Их центры определяют квадрат. В каждую из четырех окружностей вписано еще четыре окружности по такой же схеме. Если мы продолжим неограниченно вписывать окружности по этому правилу, получим последовательность. Общее число окружностей в этой последовательности, С(n), будет определяться как сумма степеней 4:

C(n) = 1 + 4 + 4² + 4³ +… + 4ⁿ = (4ⁿ⁺¹- 1)/3

Однако мастеров интересовало не столько число окружностей, сколько соотношение между их радиусами. Если мы обозначим через R радиус большой окружности, то радиусы r четырех вписанных в нее окружностей будут равны:

2R = 2r + 2r√2 = > r = R/(1 + √2)

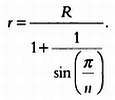
Подобная задача приведена в последней из обнаруженных на сегодняшний день сайгаку (мы уже говорили, что эта табличка была найдена в городе Тояма в 2005 году). Задача заключается в том, чтобы определить соотношение между r — радиусами восьми окружностей, расположенных в форме кольца и вписанных в другую, большую окружность, и R — радиусом большой окружности. В обобщенном варианте задачи требуется найти соотношение радиусов в случае, когда в большую окружность вписано не четыре и не восемь, а n окружностей, расположенных в форме кольца. Применив методы тригонометрии, получим решение:

Как видите, в Средние века математическая мысль существовала не только в Старом Свете. Архитектурные стили в самых разных частях мира строятся на диалоге круга и квадрата, поскольку эти геометрические фигуры играют главную роль во всех культовых сооружениях. На основе круга и (или) квадрата, параллельных и перпендикулярных прямых построены египетские пирамиды, вавилонские зиккураты, храмы, мавзолеи и другие религиозные сооружения.

Также на основе квадратов и кругов создаются самые разные трехмерные фигуры — полусферы буддийских ступ в Индии и Непале, увенчанные кубами, ступенчатые пирамиды доколумбовой Америки и даже спираль, устремленная в небо, в исламских мечетях Ближнего Востока.

Способ выражения верований — важнейшая часть культуры. Архитектура придает отношениям человека с богами осязаемую форму, и в религиозной архитектуре особую роль играет математика. В некоторых культурах математика также определяет обряды для верующих всех социальных групп. Например, на острове Бали женщины каждый день изготавливают емкости для подношений богам в форме различных геометрических фигур. При этом островитяне на практике воплощают математические идеи, воспринятые от родителей. Это знания, передаваемые из поколения в поколение, не связаны с формальной академической средой.

Человек, уважающий богов, не действует наобум. Он со всем тщанием подходит и к строительству храмов, и к посуде для подношений — если есть в жизни место совершенству, то именно в сфере религии. В свете всего вышесказанного можно утверждать, что совершенство во всех культурах связывается с геометрией, а математические идеи, созданные в разных культурах и описывающие эту взаимосвязь, объединяются понятием «этноматематика».

Глава 4

Как геометрия делает красивое прекрасным

Нельзя сказать, что использование геометрии само по себе делает вещи красивее. Но в названии этой главы мы хотим подчеркнуть, что во всех культурах высоко ценились качественно сделанные вещи, а качество во многих случаях достигалось именно благодаря математической точности. Именно в этом смысле Эрнст Гомбрих говорит о роли геометрии в искусстве в своей книге «Чувство порядка», посвященной декоративно-прикладному творчеству.